制約なし凸最適化問題に対する最急降下法と，ノルム選択，目的関数に強凸性を仮定するときの収束解析をまとめる

本記事は以下の過去記事の内容を用います．

制約なし凸最適化問題に対する最急降下法(steepest descent method)について，内容をまとめておくことにしました．Boyd and Vandenberghe(2004)の9章4節をベースにしています．なお，本記事の最急降下法におけるノルムとしてユークリッドノルムを選択したものについて，最急降下法ということも多いようです．

=================================================================================

$\;$ 0. 準備

$\;$ 1. 最急降下法
$\;\;\;$ 1.1. 理論
$\;\;\;$ 1.2. アルゴリズム

$\;$ 2. ノルム選択の例
$\;\;\;$ 2.1. ユークリッドノルム
$\;\;\;$ 2.2. 二次ノルム
$\;\;\;$ 2.3. $l_1$ ノルム

$\;$ 3. 考察
$\;\;\;$ 3.1. 収束解析
$\;\;\;$ 3.2. 二次ノルムと座標変換

[ 0. 準備 ]

冒頭の過去記事(制約なし凸最適化問題の目的関数)[ 0. 準備 ]と同じです．

冒頭の過去記事(降下法の枠組み)の内容も必要です．

[ 1. 最急降下法 ]

[ 1.1. 理論 ]

$f(x)$ の $x$ のまわりのテイラー展開の一次近似は以下です． $\langle \cdot , \cdot \rangle$ は通常の内積です．

(1.1.1) $\;\;\; f(x + v) \approx \hat{f}(x + v)$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f(x) + \nabla f(x)^T v \;\;\; \because$ テイラーの定理(文献[2])

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f(x) + \langle \nabla f(x) , v \rangle$

右辺第二項 $\nabla f(x)^T v$ は方向 $v$ における $f$ の $x$ での方向微分(directional derivative)といい，小さなステップ $v$ に対する $f$ の近似的な変化です．方向微分 $\nabla f(x)^T v$ が負の値をとるときステップ $v$ は降下方向(descent direction)です(冒頭の過去記事(降下法の枠組み)(1.1.6)にあります)．

方向微分を可能な限り負にする $v$ を選択する方法について述べます．方向微分 $\nabla f(x)^T v$ は $v$ に対して線形なので，(与えられる $v$ が降下方向，すなわち $\nabla f(x)^T v \lt 0$ であれば) $v$ を大きくすることで $\nabla f(x)^T v$ を好きなだけ負にすることができます．問いを目的にかなったものにするためには， $v$ のサイズを制限するか $v$ の長さを正規化しなければなりません．

$\left\| \cdot \right\|$ を $\mathbb{R}^n$ 上の任意のノルムとします．(ノルム $\left\| \cdot \right\|$ の意味での)正規化された最急降下方向(normalized steepest descent direction)を定義します．(複数の最急降下方向があり得ます．)

(1.1.2) $\;\;\; \Delta x_\mathrm{nsd} = \mathrm{arg \ min}_{ \{ v \ : \ \left\| v \right\| = 1 \} } \ \langle \nabla f(x) , v \rangle$

これは以下のように解釈できます． $\left\| \cdot \right\|$ ノルムの意味での単位球内で，方向 $- \nabla f(x)$ と同方向(方向 $\nabla f(x)$ と反対方向)に最大限伸ばした方向を意味します．

(1.1.3) $\;\;\; \Delta x_\mathrm{nsd} = \mathrm{arg \ min}_{ \{ v \ : \ \left\| v \right\| \le 1 \} } \ \langle \nabla f(x) , v \rangle$

$\Delta x_\mathrm{nsd}$ をスケーリングすることで得られる，正規化されていない最急降下ステップ $\Delta x_\mathrm{sd}$ を考慮すると便利です． $\left\| \cdot \right\|_{*}$ は双対ノルムです(文献[3]にあります)．

(1.1.4) $\;\;\; \Delta x_\mathrm{sd} = \left\| \nabla f(x) \right\|_{*} \Delta x_\mathrm{nsd}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \sup_{ \{ v \ : \ \left\| v \right\| \le 1 \} } \langle \nabla f(x) , v \rangle \ \Delta x_\mathrm{nsd}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \sup_{ \{ v \ : \ \left\| v \right\| \le 1 \} } \langle \nabla f(x) , v \rangle \ \mathrm{arg \ min}_{ \{ v \ : \ \left\| v \right\| \le 1 \} } \ \langle \nabla f(x) , v \rangle \;\;\; \because$ (1.1.3)

$\Delta x_\mathrm{sd}$ は， $\nabla f(x) = 0$ でないかぎり降下方向(冒頭の過去記事(降下法の枠組み)(1.1.6))であることがわかります．

(1.1.5) $\;\;\; \nabla f(x)^T \Delta x_\mathrm{sd} = \nabla f(x)^T \left\| \nabla f(x) \right\|_{*} \Delta x_\mathrm{nsd} \;\;\; \because$ (1.1.4)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| \nabla f(x) \right\|_{*} \nabla f(x)^T \Delta x_\mathrm{nsd}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| \nabla f(x) \right\|_{*} \nabla f(x)^T \ \mathrm{arg \ min}_{ \{ v \ : \ \left\| v \right\| \le 1 \} } \ \langle \nabla f(x) , v \rangle \;\;\; \because$ (1.1.3)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| \nabla f(x) \right\|_{*} \nabla f(x)^T \ \mathrm{arg \ min}_{ \{ v \ : \ \left\| v \right\| \le 1 \} } \ \nabla f(x)^T v$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| \nabla f(x) \right\|_{*} \min_{ \{ v \ : \ \left\| v \right\| \le 1 \} } \ \nabla f(x)^T v$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| \nabla f(x) \right\|_{*} \min_{ \{ v \ : \ \left\| v \right\| \le 1 \} } \ \langle \nabla f(x) , v \rangle$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| \nabla f(x) \right\|_{*} \max_{ \{ v \ : \ \left\| v \right\| \le 1 \} } \ - \langle \nabla f(x) , v \rangle$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \left\| \nabla f(x) \right\|_{*} \max_{ \{ v \ : \ \left\| v \right\| \le 1 \} } \ \langle \nabla f(x) , v \rangle$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \left\| \nabla f(x) \right\|_{*} \sup_{ \{ v \ : \ \left\| v \right\| \le 1 \} } \ \langle \nabla f(x) , v \rangle$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \left\| \nabla f(x) \right\|_{*} \left\| \nabla f(x) \right\|_{*} \;\;\; \because$ 双対ノルムの定義(文献[3])

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \left\| \nabla f(x) \right\|_{*}^2$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \lt 0$

[ 1.2. アルゴリズム ]

最急降下法は探索方向に最急降下方向 $\Delta x_\mathrm{sd}$ を用います．アルゴリズムを以下に示します．厳密直線探索(exact line search)とバックトラッキング直線探索(backtracking line search)は冒頭の過去記事(降下法の枠組み)にあります．

f:id:seetheworld1992:20201124160106p:plain

厳密直線探索(冒頭の過去記事(降下法の枠組み)(1.2.1))を用いるときは，スケールファクターの効果はないので $\Delta x_\mathrm{nsd}$ と $\Delta x_\mathrm{sd}$ の区別はありません．

[ 2. ノルム選択の例 ]

最急降下方向を決定するときに用いるノルムによって，最急降下方向が変わります．本章では，いくつかのノルムについて，それらを選択する場合の性質を調べていきます．

[ 2.1. ユークリッドノルム ]

ノルム $\left\| \cdot \right\|$ としてユークリッドノルム $\left\| \cdot \right\|_{2}$ を選択すると，双対ノルム $\left\| \cdot \right\|_{*} = \left\| \cdot \right\|_{2}$ です(文献[3]にあります)．このとき以下を得ます．この $\Delta x_\mathrm{sd}$ は勾配降下法(gradient descent method)(冒頭の過去記事(制約なし凸最適化問題に対する勾配降下法)(1.1.1))に一致します．したがって，勾配降下法は最急降下法の特別な場合であることがわかります．

(2.1.1) $\;\;\; \Delta x_\mathrm{nsd} = \mathrm{arg \ min}_{ \{ v : \left\| v \right\|_2 = 1 \} } \ \langle \nabla f(x) , v \rangle \;\;\; \because$ (1.1.2) $, \ \left\| \cdot \right\| = \left\| \cdot \right\|_2$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \frac{ \nabla f(x) }{ \left\| \nabla f(x) \right\|_2 }$

(2.1.2) $\;\;\; \Delta x_\mathrm{sd} = \left\| \nabla f(x) \right\|_{*} \Delta x_\mathrm{nsd}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| \nabla f(x) \right\|_{2} \Delta x_\mathrm{nsd} \;\;\;\;\;\; \because \left\| \cdot \right\|_{*} = \left\| \cdot \right\|_2$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| \nabla f(x) \right\|_{2} \left[ - \frac{ \nabla f(x) }{ \left\| \nabla f(x) \right\|_2 } \right] \;\;\; \because$ (2.1.1)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \nabla f(x)$

[ 2.2. 二次ノルム ]

ノルム $\left\| \cdot \right\|$ として二次ノルム(quadratic norm)(冒頭の過去記事(二次ノルムの定義)定義.にあります) $\left\| \cdot \right\|_{P}$ を選択すると，任意の $x \in \mathbb{R}^n$ について双対ノルム $\left\| x \right\|_{*} = \left\| P^{-1/2} x \right\|_{2}$ です(冒頭の過去記事(二次ノルムの双対ノルム)事実.にあります)．このとき以下を得ます．

(2.2.1) $\;\;\; \Delta x_\mathrm{nsd} = \mathrm{arg \ min}_{ \{ v \ : \ \left\| v \right\|_{P} = 1 \} } \ \langle \nabla f(x), v \rangle$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \mathrm{arg \ min}_{ \{ v \ : \ \left\| P^{1/2} v \right\|_2 = 1 \} } \ \langle \nabla f(x), v \rangle$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \mathrm{arg \ min}_{ \{ v \ : \ \left\| P^{1/2} v \right\|_2 = 1 \} } \ \nabla f(x)^T v$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \mathrm{arg \ min}_{ \{ v \ : \ \left\| P^{1/2} v \right\|_2 = 1 \} } \ \nabla f(x)^T P^{-1/2} P^{1/2} v$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \mathrm{arg \ min}_{ \{ v \ : \ v = P^{-1/2} \ y, \ \left\| y \right\|_2 = 1 \} } \ ( \nabla f(x)^T P^{-1/2} ) y$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \mathrm{arg \ min}_{ \{ v \ : \ v = P^{-1/2} \ y, \ \left\| y \right\|_2 = 1 \} } \ y^T ( \nabla f(x)^T P^{-1/2} )^T$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \mathrm{arg \ min}_{ \{ v \ : \ v = P^{-1/2} \ y, \ \left\| y \right\|_2 = 1 \} } \ y^T (P^{-1/2} \nabla f(x)) \;\;\; \because (P^{-1/2})^T = P^{-1/2}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = P^{-1/2} \left[ - \frac{ P^{-1/2} \nabla f(x) }{ \left\| P^{-1/2} \nabla f(x) \right\|_2 } \right]$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \frac{ P^{-1} \nabla f(x) }{ \left\| P^{-1/2} \nabla f(x) \right\|_2 }$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - P^{-1} \nabla f(x) / \left[ \left\| P^{-1/2} \nabla f(x) \right\|_2^2 \right]^{1/2}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - P^{-1} \nabla f(x) / \left[ ( P^{-1/2} \nabla f(x) )^T ( P^{-1/2} \nabla f(x) ) \right]^{1/2}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - P^{-1} \nabla f(x) / \left[ \nabla f(x)^T P^{-1/2} P^{-1/2} \nabla f(x) \right]^{1/2} \;\;\; \because (P^{-1/2})^T = P^{-1/2}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - P^{-1} \nabla f(x) / \left[ \nabla f(x)^T P^{-1} \nabla f(x) \right]^{1/2}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \left[ \nabla f(x)^T P^{-1} \nabla f(x) \right]^{-1/2} P^{-1} \nabla f(x)$

(2.2.2) $\;\;\; \Delta x_\mathrm{sd} = \left\| \nabla f(x) \right\|_{*} \Delta x_\mathrm{nsd} \;\;\;\;\;\; \because$ (1.1.4)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| P^{-1/2} \nabla f(x) \right\|_{2} \Delta x_\mathrm{nsd} \;\;\; \because \forall x \in \mathbb{R}^n, \ \left\| x \right\|_{*} = \left\| P^{-1/2} x \right\|_{2}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - P^{-1} \nabla f(x) \;\;\;\;\;\;\;\;\; \because$ (2.2.1)

二次ノルムの意味での正規化された最急降下方向 $\Delta x_\mathrm{nsd}$ の概念を図示すると以下です．

f:id:seetheworld1992:20201127190634p:plain

次に，二次ノルムの意味での最急降下方向 $\Delta x_\mathrm{sd}$ を，座標変換を行った後の凸最適化問題に対する勾配降下法による探索方向と解釈する場合について考えます．以下の座標変換を考えます． $u,\bar{u} \in \mathbb{R}^n$ です．

(2.2.3) $\;\;\; \bar{u} = P^{1/2} u$

元の座標系における点 $u$ の二次ノルムは座標変換後の座標系における点 $\bar{u}$ のユークリッドノルムに一致します．

(2.2.4) $\;\;\; \left\| u \right\|_P = \left\| P^{1/2} u \right\|_2$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| \bar{u} \right\|_2 \;\;\; \because$ (2.2.3)

この座標変換(2.2.3)を用いる，元の凸最適化問題と等価な凸最適化問題を考えると，その問題を解くことにより，元の問題を解くことができます．そのために関数 $\bar{f} : \mathbb{R}^n \to \mathbb{R}$ を以下で定義します．

(2.2.5) $\;\;\; \bar{f} ( \bar{u} ) = f ( P^{-1/2} \bar{u} )$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f ( u ) \;\;\; \because$ (2.2.3)

$\bar{f}$ に勾配降下法(冒頭の過去記事(制約なし凸最適化問題に対する勾配降下法)(1.1.1))を適用するとき，点 $\bar{x}$ (元の座標系における点 $x = P^{-1/2} \bar{x}$ に対応します) における探索方向は以下です．元の凸最適化問題の探索方向も得ます．

(2.2.6) $\;\;\; \Delta \bar{x} = - \nabla \bar{f} ( \bar{x} )$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \left( P^{-1/2} \right)^T \nabla f ( P^{-1/2} \bar{x} ) \;\;\; \because$ 連鎖律(文献[7])

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - P^{-1/2} \nabla f ( P^{-1/2} \bar{x} ) \;\;\; \because P^T = P$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - P^{-1/2} \nabla f(x)$

(2.2.7) $\;\;\; \Delta x = P^{-1/2} \Delta \bar{x} \;\;\; \because$ (2.2.3)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = P^{-1/2} \left[ - P^{-1/2} \nabla f(x) \right] \;\;\; \because$ (2.2.6)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - P^{-1} \nabla f(x)$

この $\Delta x$ は(2.2.2)に一致します．いいかえると，二次ノルム $\left\| \cdot \right\|_P$ の意味での最急降下法は，座標変換 $\bar{x} = P^{1/2} x$ を行った凸最適化問題に対する勾配降下法(を元の座標系から見たもの)として考えることができます．

[ 2.3. $l_1$ ノルム ]

ノルム $\left\| \cdot \right\|$ として $l_1$ ノルム(文献[4]にあります) $\left\| \cdot \right\|_1$ を選択すると，双対ノルム $\left\| \cdot \right\|_{*} = \left\| \cdot \right\|_{\infty}$ です(文献[3][4]にあります)．以下のような $i$ を定義します． $( \cdot )_j$ はベクトルの第 $j$ 要素です．

(2.3.0) $\;\;\; i = \{ j \in \{ 1,2,\ldots,n \} \ | \ \left\| \nabla f(x) \right\|_\infty = | ( \nabla f(x) )_j | \}$

このとき以下を得ます． $e_j$ は標準基底です(文献[5]にあります)．

(2.3.1) $\;\;\; \Delta x_\mathrm{nsd} = \mathrm{arg \ min}_{ \{ v \ : \ \left\| v \right\|_1 = 1 \} } \ \langle \nabla f(x), v \rangle$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \mathrm{arg \ min}_{ \{ v \ : \ \sum_{j=1}^n | v_j | = 1 \} } \ \langle \nabla f(x), v \rangle$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \mathrm{ sgn } \left[ ( \nabla f(x) )_i \right] e_i$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \mathrm{ sgn } \left( \frac{\partial f(x)}{\partial x_i} \right) e_i$

(2.3.2) $\;\;\; \Delta x_\mathrm{sd} = \left\| \nabla f(x) \right\|_{*} \Delta x_\mathrm{nsd} \;\;\; \because$ (1.1.4)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left\| \nabla f(x) \right\|_{\infty} \Delta x_\mathrm{nsd}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \max \left\{ \left| \frac{\partial f(x)}{\partial x_1} \right| , \ldots , \left| \frac{\partial f(x)}{\partial x_n} \right| \right\} \ \Delta x_\mathrm{nsd}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \left| \frac{\partial f(x)}{\partial x_i} \right| \Delta x_\mathrm{nsd} \;\;\;\;\;\;\;\;\; \because$ (2.3.0)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \left| \frac{\partial f(x)}{\partial x_i} \right| \ \mathrm{ sgn } \left( \frac{\partial f(x)}{\partial x_i} \right) e_i \;\;\; \because$ (2.3.1)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = - \frac{\partial f(x)}{\partial x_i} e_i, \;\;\;\;\;\; i = \left\{ j \in \{ 1,2,\ldots,n \} \ | \ \left\| \nabla f(x) \right\|_\infty = \left| \frac{\partial f(x)}{\partial x_i} \right| \right\}$

このように， $l_1$ ノルムの意味での最急降下法は常に標準基底(あるいは負の標準基底)を選択するものです．それは $f$ の近似的な変化すなわち(1.1.1)右辺第二項 $\nabla f(x)^T v$ を最小化する座標軸の方向を意味します．

$l_1$ ノルムの意味での正規化された最急降下方向 $\Delta x_\mathrm{nsd}$ の概念を図示すると以下です．

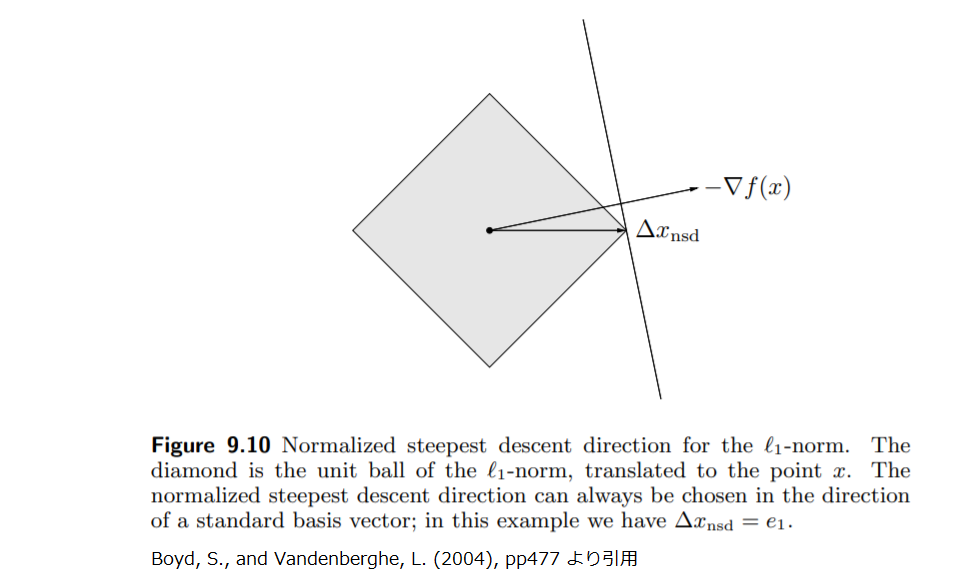
f:id:seetheworld1992:20201129192112p:plain

$l_1$ ノルムの意味での最急降下法は自然な解釈を持ちます: 各反復において $\nabla f(x)$ の要素の中で絶対値が最大となるものを選択し，その $(\nabla f(x))_i$ の符号にしたがって $x_i$ を増加あるいは減少させます．このアルゴリズムは各反復において $x$ の一つの要素のみ更新するので，座標降下法(coordinate descent algorithm)といいます．これは厳密直線探索を非常に簡単にすることができます．

[ 3. 考察 ]

[ 3.1. 収束解析 ]

目的関数に強凸性を仮定し，最急降下法とバックトラッキング直線探索を用いるとします．この設定の下，任意のノルム $\left\| \cdot \right\|$ の意味での収束について調べていきます．勾配降下法(冒頭の過去記事(制約なし凸最適化問題に対する勾配降下法)にあります)の収束解析の拡張になっています．

ノルムの同値性(equivalence of norms)を用います(文献[4]にあります)．有限次元ノルム空間において任意のノルムは互いに同値なので， $\mathbb{R}^n$ 上の任意のノルムはユークリッドノルムで抑えられます．したがって以下を得ます．

(3.1.1.a) $\;\;\; \exists \gamma \in (0, 1 ], \;\;\; \gamma \left\| x \right\|_2 \le \left\| x \right\|$

(3.1.1.b) $\;\;\; \exists \tilde{\gamma} \in (0, 1 ], \;\;\; \tilde{\gamma} \left\| x \right\|_2 \le \left\| x \right\|_*$

目的関数 $f$ は劣位集合(冒頭の過去記事(制約なし凸最適化問題の目的関数)(0.2.1)にあります) $S$ 上で強凸(strongly convex)であると仮定します．強凸性を仮定することにより得られる不等式である冒頭の過去記事(制約なし凸最適化問題の目的関数)(1.2.2)で， $y = x + t \Delta x_\mathrm{sd}$ として以下を得ます．

(3.1.2) $\;\; f(y) \le f(x) + \nabla f(x)^T (y - x) + \frac{M}{2} \left\| y - x \right\|_2^2$

$\;\;\; \Rightarrow \ f(x + t \Delta x_\mathrm{sd}) \le f(x) + \nabla f(x)^T \left( t \Delta x_\mathrm{sd} \right) + \frac{M}{2} \left\| t \Delta x_\mathrm{sd} \right\|_2^2$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f(x) + t \nabla f(x)^T \Delta x_\mathrm{sd} + \frac{M t^2 }{2} \left\| \Delta x_\mathrm{sd} \right\|_2^2$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f(x) - t \left\| \nabla f(x) \right\|_{*}^2 + \frac{M t^2 }{2} \left\| \Delta x_\mathrm{sd} \right\|_2^2 \;\;\; \because$ (1.1.5)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \le f(x) - t \left\| \nabla f(x) \right\|_{*}^2 + \frac{M t^2 }{2} \left[ \frac{1}{\gamma} \left\| \Delta x_\mathrm{sd} \right\| \right]^2 \;\;\; \because$ (3.1.1.a)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f(x) - t \left\| \nabla f(x) \right\|_{*}^2 + \frac{M t^2 }{2} \left[ \frac{1}{\gamma} \left\| \left\| \nabla f(x) \right\|_{*} \Delta x_\mathrm{nsd} \right\| \right]^2 \;\;\; \because$ (1.1.4)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f(x) - t \left\| \nabla f(x) \right\|_{*}^2 + \frac{M t^2 }{2} \left[ \frac{1}{\gamma} \left\| \nabla f(x) \right\|_{*} \left\| \Delta x_\mathrm{nsd} \right\| \right]^2$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f(x) - t \left\| \nabla f(x) \right\|_{*}^2 + \frac{ M t^2 }{2} \left[ \frac{1}{\gamma} \left\| \nabla f(x) \right\|_{*} \right]^2 \;\;\; \because$ (1.1.2)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f(x) - t \left\| \nabla f(x) \right\|_{*}^2 + \frac{ M }{2 \gamma^2 } t^2 \left\| \nabla f(x) \right\|_{*}^2 \;\;\;\;\;\;$ (3.1.2)(※)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{M}{ 2 \gamma^2 } \left\| \nabla f(x) \right\|_*^2 \left( t - \frac{\gamma^2}{M} \right)^2 + f(x) - \frac{\gamma^2}{2M} \left\| \nabla f(x) \right\|_*^2 \;\;\;\;\;\;$ (3.1.2)(※※)
$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \because$ 冒頭の過去記事(制約なし凸最適化問題に対する勾配降下法)(2.1.3)と同様の式変形

(3.1.3) $\;\;\; f(x^{+}) = f( x + t \Delta x_\mathrm{sd} )$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \le f(x) - \min \{ \alpha , \beta \gamma^2 \alpha / M \} \left\| \nabla f(x) \right\|_*^2$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f(x) - \alpha \min \{ 1 , \beta \gamma^2 / M \} \left\| \nabla f(x) \right\|_*^2$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \le f(x) - \alpha \min \{ 1 , \beta \gamma^2 / M \} \ \tilde{\gamma}^2 \left\| \nabla f(x) \right\|_2^2 \;\;\; \because$ (3.1.1.b)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f(x) - \alpha \tilde{\gamma}^2 \min \{ 1 , \beta \gamma^2 / M \} \left\| \nabla f(x) \right\|_2^2$

$\;\;\; \Leftrightarrow \ f(x^{+}) - p^* \le f(x) - p^* - \alpha \tilde{\gamma}^2 \min \{ 1 , \beta \gamma^2 / M \} \left\| \nabla f(x) \right\|_2^2$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \le f(x) - p^* - \alpha \tilde{\gamma}^2 \min \{ 1 , \beta \gamma^2 / M \} \left[ 2m(f(x)-p^*) \right]$
$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \because$ 冒頭の過去記事(制約なし凸最適化問題の目的関数)(1.1.5)

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = f(x) - p^* - 2 m \alpha \tilde{\gamma}^2 \min \{ 1 , \beta \gamma^2 / M \} (f(x)-p^*)$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = (1 - 2 m \alpha \tilde{\gamma}^2 \min \{ 1 , \beta \gamma^2 / M \} )(f(x) - p^*)$

以下を定義します．

(3.1.4) $\;\;\; c = 1 - 2 m \alpha \tilde{\gamma}^2 \min \{ 1 , \beta \gamma^2 / M \} \; ( \lt 1 )$

したがって冒頭の過去記事(制約なし凸最適化問題に対する勾配降下法)(2.2.4)(※)あるいは同記事(2.3.9)とほぼ同じ以下を得ます．これは勾配降下法と同様に一次収束です．

(3.1.5) $\;\;\; f(x^{(k)}) - p^* = c^k ( f(x^{(0)}) - p^* )$

$\;\;\;\;\; \Rightarrow \;\;\; \lim_{k \to \infty} f(x^{(k)}) = p^*$

[ 3.2. 二次ノルムと座標変換 ]

最急降下法のノルム選択は収束の速さに大きな影響を与えます．簡単のため，最急降下法のノルムに $P$ -二次ノルムを選択した場合について考えます．本記事[ 2.2. 二次ノルム ]で示したように，この場合の最急降下法は座標変換(2.2.3)を行った座標系における最適化問題に勾配降下法を適用した場合と等価です．冒頭の過去記事(制約なし凸最適化問題に対する勾配降下法)にあるように，勾配降下法は劣位集合(あるいは最適点の付近のヘッセ行列)の条件数が適度であれば上手くいき，大きければ上手くいきません．したがって，座標変換 $\bar{x} = P^{1/2} x$ を行った後の劣位集合の条件数が適度であれば最急降下法は上手くいきます．

ここまでの考察は行列 $P$ の選択の方針を与えます: $P$ は座標変換を行った後の劣位集合の条件数が適切になるように選択すべきです． $\bar{f}$ のヘッセ行列は以下です．

(3.2.1) $\;\;\; \nabla^2 \bar{f}(\bar{x}) = \left( P^{-1/2} \right)^T \nabla^2 f( P^{-1/2} \bar{x} ) P^{-1/2} \;\;\; \because$ 連鎖律(文献[7])

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = P^{-1/2} \ \nabla^2 f( P^{-1/2} \bar{x} ) P^{-1/2} \;\;\; \because P^T = P$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = P^{-1/2} \ \nabla^2 f(x) \ P^{-1/2}$

たとえば最適点 $x^*$ における $f$ のヘッセ行列 $\nabla^2 f(x^*)$ の近似 $\hat{H}$ を既知とするとき，非常に良い $P$ の選択は $P = \hat{H}$ です．このとき $\bar{f}$ のヘッセ行列は最適点 $\bar{x}^* = P^{1/2} x^*$ に近い範囲では単位行列 $I$ となり，したがって条件数は $1$ です． $\bar{x}^*$ に近い範囲では劣位集合が点 $\bar{x}^*$ を中心とする球で近似できることを意味します．

(3.2.2) $\;\;\; \nabla^2 \bar{f}(\bar{x}^*) = P^{-1/2} \nabla f(x^*) P^{-1/2}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \hat{H}^{-1/2} \nabla f(x^*) \hat{H}^{-1/2}$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \approx I$

座標変換を用いずに同じことがいえます．座標変換 $\bar{x} = P^{1/2} x$ を行った後の劣位集合の条件数が小さいことは以下の楕円 $\mathcal{E}$ が座標変換を行う前の劣位集合の形のよい近似になっていることと等価です．(いいかえると，この楕円に適切なスケーリングと平行移動を行うと座標変換を行う前の劣位集合のよい近似になっています．)(この楕円を座標変換すると球に近いです．)